塾の問題に挑戦しよう!(数列編)
1.とある学校近隣塾の配布物より
■よく学校周辺の塾の方が校門前で、塾の案内チラシを配っておられるシーンに出くわしますね。子どもたちがもらってきたプリントに挑戦してみましょう。
その問題とは、こんな問題でした。
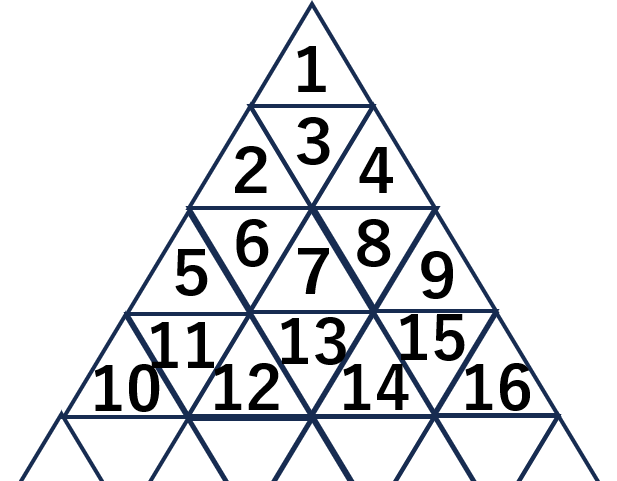
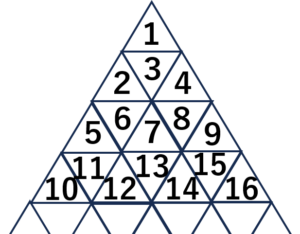
【問題】図のように、三角形のカードを並べて、1段目に1,2段目に2,3,4、3段目に5.6,7,8、9のように書いていきます。これについて、次の問いに答えましょう。
(1)7段目の一番右にある数は何ですか。
(2)10段目の真ん中にある数は何ですか。
(3)135は何段目の左から何番目にありますか。
 数列
数列
2.問題に挑戦
■表や絵にしたり、線分図を書いたりして、算数の問題はといていくのでした。
合言葉はこれです。
・具体的に解いていく ・順序よく解いていく
■このような、数が連続で出てくる問題は、表に書いて考えると、見えてきます。
横に、段数を書いていき、縦に何をとるかというと、それは小さい問題によって決定されます。
つまり、小問に、(1)は右側の数字を、(2)は真ん中の数字を、(3)はその合体編と左側の数字となっています。
それで、縦軸としては、左側の数字、右側の数字、中央の数字と、表してやっていきましょう。
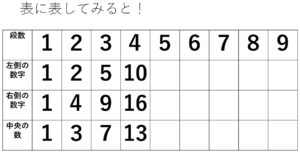
すると、こんな表になりますね。
 表
表問題図を見ると、上の表までは作成できますよね。今、横軸の4段目まで図から完成しています。
これで終了してはいけません。もう1段位、数値を付け加えないと、本当にそうかというのがわかりません。よって、図に手書きをして、もう1段、つまり5段目がどうなるか、数値をいれていきましょう。そうすれば、関係がはっきりとしてくるかと思います。
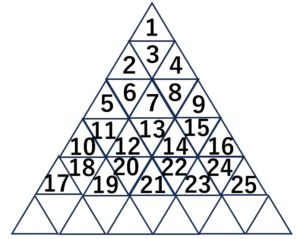
やってみましょう。
 三角形追加
三角形追加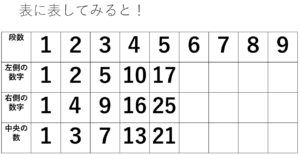 表
表これで、少し関係がみえてきましたよね。表で、一番大切なことは、次のことです。
となりとの差をとれ→表に記入せよ
ということです。
その差を次のように、間に書き込んでいくといいですよ。
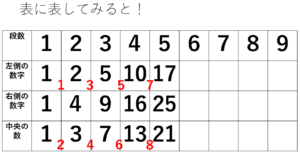
■高校では、ここから「漸化式」といって、公式めいたものを作ることになりますが、ここは小学生ですので、上の表を元に、小問題に答えてみましょう。
3.問題を解く!
(1)各段の右側は、(段数)✕(段数)になっているというのがわかります。それで、7段目なので、7✕7=49 答えは、49ということになりますね。
(2)各段の中央値は、2からの偶数で増えていっていることがわかります。上の表では、5段目までがわかっていますので、順に10段目までいけばわかりますね。
21+10+12+14+16+18=91 となりますね。
式でやるとすれば、1から始まって、2からの偶数を順に9回(2✕9まで)足すことになりますよね。ずっと足していくと、大変なので、以下のように逆にして2段上下で足していくと、どこも「20」となりますよね。
2段目・・・・・・・・・・・・・・10段目
2+4+6+8+10+12+14+16+18
18+16+14+12+10+8+6+4+2
だから、20✕9(回)=180
往復2回足しているので、180➗️2=90
最後に最初の1を足せばいいので、90+1=91 答えは91です。
(3)12✕12=144なので、135は、この12段の中にあるということになります。中央値から考えてもいいし、左側の数値から考えてもいいですね。左側の数字から考えてみましょう。
先程と同じように、左側の数字は、1から始まる奇数の合計となっています。
2段目・・・・・・・・・・・・・・・・・・12段目
1+3+5+7+9+11+13+15+17+19+21
21+19+17+15+13+11+9+7+5+3+1
22✕11➗️2+1=121
135-121=14 だから、12段目の左から14番目ということになります。
4.まとめ
具体的に、図や表を使って、根気よく順に処理していきましょう。そして、もしわかったら、式にしてみましょう。



