小学校算数科の鉄則シリーズー鉄則4:角度の公式-

目次
鉄則4:角度の公式
鉄則4-1:三角形の内角の和は180°
鉄則4-2:正N角形の中心角は、360°÷N
鉄則4-3:N角形の内角の和は、180×(N-2)
鉄則4-4:正N角形の内角は、180×(N-2)÷N
■それでは早速、公式の意味を確認していきましょう。
鉄則4-1:三角形の内角の和は、180°
■2枚の三角定規を出してみましょう。
1つは30°ー60°ー90°ですよね。もう1つは、45°ー45°ー90°でしたよね。
つまり、合計すると、どちらも180°となりますね。
・どんな三角形も、3つの角度を足し合わせると、180°になります。
(例題)次の角いの大きさを求めましょう。
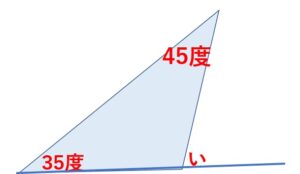 三角形の角度問題
三角形の角度問題まずは、角いのとなりの角度を求めましょう。すると、こうなりますよね。
180ー(34+45)=100
角いのとなりは100°とわかりました。一直線は180°でしたから、角いは次の式で求められますね。
180ー100=80
80°ということになります。実は、このような2段かまえでとくより、次の1文を覚えておくと、すぐとけますよ。
・三角形の外角(角い)は、そのとなりにない内角の和(35+45)に等しい
外側の角度のことを外角、内側の角度のことを内角といいます。角いは外角ですので、いきなり、次の式で求めることができます。つまり、他の2つの内角を足し合わせればいいというわけです。
35+45=80 答え 80°
鉄則4-2:正N角形の中心角は、360°÷N
次の正六角形を見てください。中心角と内角というのがどこにあたるのかを、確認してください。
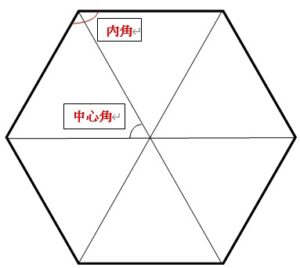 正六角形
正六角形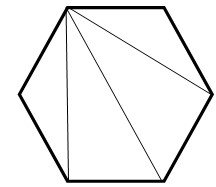
ここでは正六角形で考えてみましょう。Nの代わりに、6なわけです。
それでまずは、中心角ですが、図の通り、同じ角度が6つあって、それが360°を囲んでいるわけですね。だから、1つの中心角は、
360÷6=60
となるわけです。公式通りですね。
鉄則4-3:N角形の内角の和は、180×(N-2)
今度は「正」がついていませんが、上の図、正六角形で考えてみましょう。
三角形の内角の和は180°でした。なので、(正)六角形を三角形に分けてみましょう。すると、右側の図のように、4つの三角形からできているのがわかりますよね。
だから、180×4=720
となります。これは、五角形だと3つの三角形、四角形だと2つの三角形からなっています。つまり、Nー2の三角形からできているということになります。
そこで、上の公式が成り立つわけですね。
鉄則4-4:正N角形の内角は、180×(N-2)÷N
三角形だと内角は3つ、四角形だと4つ、五角形だと5つ、六角形だと6つなので、その数(N)で内角の和をわればいいということになります。
上の図の正六角形だと、まずは内角の和が今、求めたように、180×(6-2)=720
これを「正」がついているので、6つの内角のうちの1つ分なので、6で割るといいということになります。
まとめると、こうなります。
180×(6-2)÷6=120 答え 120°
練習問題をやってみましょう。
正五角形があります。
1)中心角を求めましょう。
2)内角の和を求めましょう。
3)1つの内角の大きさを求めましょう。
それぞれ、公式に当てはめてみましょう。
1)360÷5=72 答え72°
2)180×(5-2)=540 答え540°
3)540÷5=108 答え108°
その他、角度の問題がいくつかありますので、以下のプリントをダウンロードして挑戦してみましょう。
平行四辺形には、角度の特色がありますので、以下のプリントをダウンロードして、ぜひ挑戦してみてくださいね。
■最後に、鉄則4を振り返ります。
鉄則4-1:三角形の内角の和は180°
鉄則4-2:正N角形の中心角は、360°÷N
鉄則4-3:N角形の内角の和は、180×(N-2)
鉄則4-4:正N角形の内角は、180×(N-2)÷N





